パチンコの確率変動の 平均継続回数 はどのように求めるのでしょうか。
実際、確率変動は理論的には無限に続く可能性があります。

それなのに確率変動の「（期待）平均継続回数」が求められるということに疑問を持ったことはないでしょうか。

実はこれ、高校数学Ⅲで学習する「無限等比級数、等比数列」という考え方で説明がつくのです。

遊技機のシミュレーションでは必ず使う概念なので、できればこの計算式も理解を深めていただきたいと思います。

CR真北斗無双　シミュレーション
P牙狼-冴島鋼牙-、大当たり継続回数の計算方法
PA大工の源さん　継続回数の計算

■　無限に続く場合は「代数」という考え方を使う

まずは求めたいものをいったんアルファベットに置き換えます。

・確変継続回数　S
・大当たり　　　a
・確変継続率　　r

ここでは分かり易いように確変継続率r＝50％とします。
確変は無限に続くのですから、

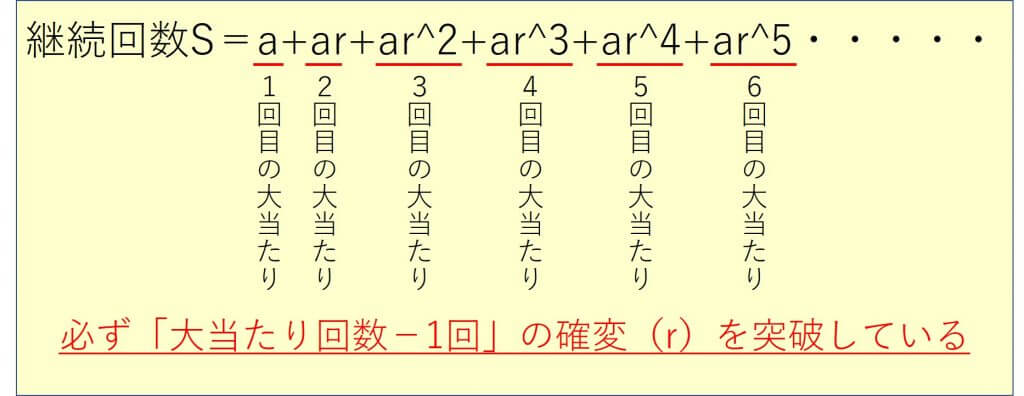
S＝a+ar+ar^2+ar^3+ar^4+ar^5・・・・・（以下無限に続く） →　①

と表せます。

数式だと少し分かりづらいのですが、必ず「大当たり回数－1回の確変を突破」することになるのです。（単発のときの突破は0回ですね）

ここで上記の式の両辺に「r」を掛けてみます。
右辺と左辺両方にrを掛けるので、

Sr＝ar+ar^2+ar^3+ar^4+ar^5+ar^6・・・・・（以下無限に続く）　→　②

となります。

この①式と②式を比べると面白いことに気づきます。

なんと、①式のar以降と②式のすべてが全く同じになるのです。

つまり②式のすべてが「Sｒ」ということなのです。

こうなると②式を①式に代入できます。

S＝a+Sr

この式の左辺と右辺を入れ替えて展開していくと、

S－Sr＝a

（1－r）S＝a

となるので、Ｓすなわち無限等比級数は

S＝a÷（1-r）

と展開できます。
ここでアルファベットを本来の意味に戻します。
　
・確変継続回数　S
・大当たり　　　a
・確変継続率 r

ですから、

確変継続回数＝大当たり÷（1－確変突入率）

となり大当たり＝aは必ず毎回「1」なので、

確変継続回数＝1÷（1－確変突入率）

となるのです。

細かい計算を文字に起こした記事なので分かりにくい点が多々あるかと思います。　
疑問点などありましたら、お問い合わせページからお気軽にご相談をしていただければと思います。

計数管理をしっかりとマスターして、稼働と利益の両立を図りましょう。
　
　
（了）
　
　

■　自店の力はどのくらい？御社の課題を炙り出し