BY の重要性
この文章は月刊アミューズメントジャパン誌にて連載されている「基礎から再確認、計数管理」の第11回、2020年4月号に掲載されたものです。
改めてウェブ上にアップすることで連載内容のおさらいになるかな、と思いますので、今後も定期的にアミューズメントジャパン誌の連載をアップしてまいります。
皆さん、こんにちは。アミューズメントビジネスコンサルティング株式会社の林秀樹です。
計数管理に対して苦手意識を持つ方も多いと思います。この連載ではそういった苦手意識を克服していただくために、分かり易くお伝えしています。今回はベース(B)の構成要素となる「BY」についてお伝えします。
■ BY は利益に直結
BYとは、ベース(B)のうちスタート(S)にかかる賞球以外の払い出しの事を指します。例えばスタート入賞口の払い出しが4個の機種でスタート回数が5.0回/分、ベースが30.0%だとすると、
BY=B-(S×賞球数)
=30.0-(5.0×4)
=10.0(%)
となります。
ここで図①を見てください。
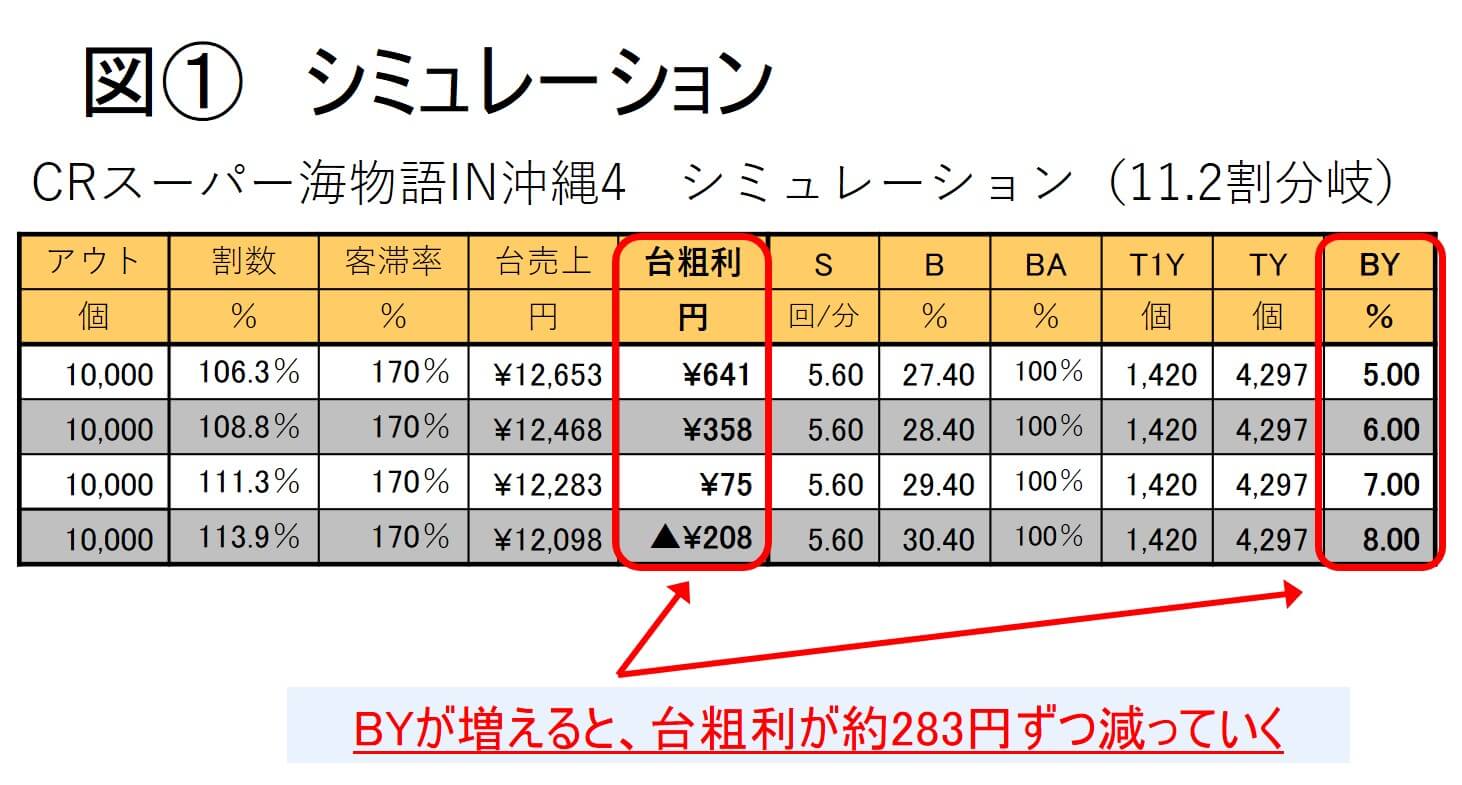
CRスーパー海物語in沖縄4において、BYの変化が割数や粗利益に及ぼす影響をシミュレーションしたものです(アウト10,000、スタートを5.60回に固定)。
このシミュレーションから例えばBYが1.0変化すると、スタート回数その他の条件が同じであっても粗利益が約283円ずつ減少していることがわかります。
CRスーパー海物語in沖縄4が10台設置されていると283円×10台で一日あたり2,830円の粗利益ロスです。
さらに1ヶ月(30日)では84,900円(2,830円×30日)、1年ではなんと101万8,800円(84,900円×12ヶ月)もの粗利益をロスしているのです。
もちろん導入した台の全てが店舗で定めたBYを超えているとは限りません。しかし店舗の4円パチンコ総台数が200台だとしてそのたった5%が基準値を1.0上回っているとすると、上記のように年間約100万円のロスとなっているのです。
■ 粗利が増える⇒遊技客の負担が増える?
これまで述べたようにBYを減らすことで粗利ロスを減らすことができますが、ここで新たな疑問も出てきます。すなわち、
・粗利が増えるということはそれだけお客様に過度な負担を強いていないだろうか
というものです。
しかし、実はBYを減らしてもそれほど大きな負担増ではないのです。
BYが1.0%減るということは、吸い込み率(B%)が1.0%上がることを意味しています。
例)S 5.0回/分 賞球4個のとき
・BY5.0 ⇒ B%=100%-(5.0×4+5.0)=75.0%
・BY4.0 ⇒ B%=100%-(5.0×4+4.0)=76.0%
BYが1.0減ると遊技客はそれまでよりも1分間に1発多く吸い込まれます。4円パチンコでは1分間に4円多く使う、1時間では240円(4円×60個)多く使う計算です。1時間でおおよそ1万5000円~2万円程度使用する現在のパチンコにおいて、これまでよりも1時間に240円の負担増がわかるか、といえば、そのようなことはないといえるでしょう。
■ Bと遊技時間の関係
「Bを高めると1,000円あたりに遊べる時間が長くなるので、遊技客の満足度は高まるのでは?」
このように考える方もいるかもしれません。BYをあえて高く設定しお客様の負担を少なくしようという目的です。しかし同じ額の粗利益を確保するためには、何かを上げれば何かを下げなくてはいけません。この場合にSとBの関係で考えると、
・Bを高めるならSを抑える
・Bを抑えるならSを上げられる
となります。このとき初当りを得るまでに必要な投資金額は、実はどちらもまったく同じなのです(図②)。
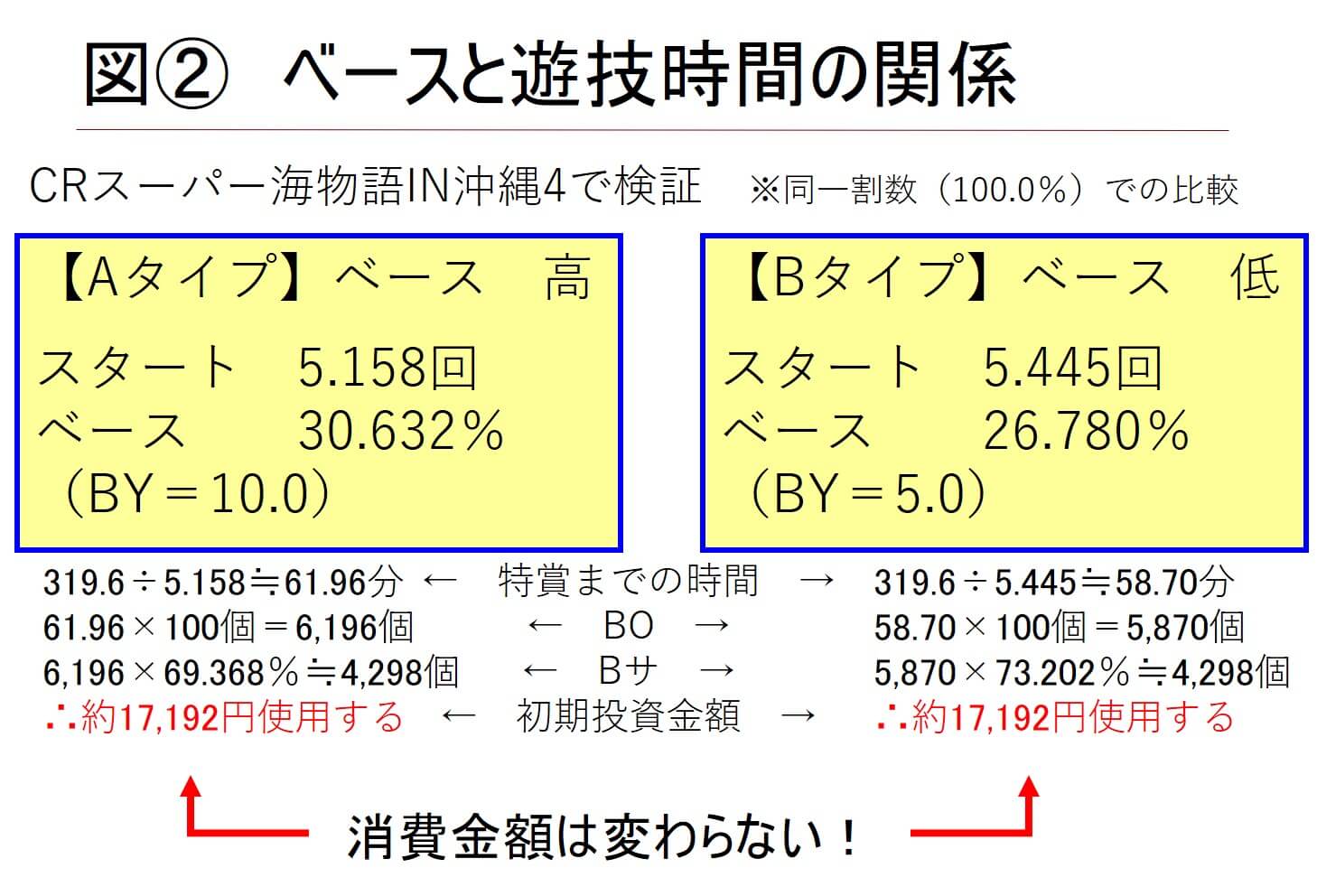
また、Bを高めると確かに1,000円で遊技できる時間は増えますが、逆に大当たりするまでの時間が長くかかってしまいます。
一般的に満足度は「満足度=F/C」であらわされます。Fとは「ファンクション(機能、便益)」、Cとは「コスト」を表します。分数の計算式で数値が大きくなるためには、分子が大きくなるか分母が小さくなればよいので、
・同じコストがかかる場合、より多くの便益があるほうが高まる(Fが大きくなればよい)
・同じ便益が得られる場合、より少ないコストのほうが高まる(Cが小さくなればよい)
といわれます。大当たりまでにかかる金額が同じならば(=同じ便益ならば)、少しでも短い間隔のほうが(=「時間」というコストが少ないほうが)満足度は高まると考えられます。

このように、Bを高めたとしてもそのままお客様の満足度アップにはつながらないのです。
【今回のポイント】
・BYは利益に直結する
・Bが高くても満足度は高まらない
(了)




